Zaciekawić matematyką: maja 2015

poniedziałek, 25 maja 2015

Trójkąt sferyczny

Trójkąt sferyczny to figura przestrzenna powstała z trzech łuków kół wielkich na sferze. Łuki te spełniają tę samą funkcję, co odcinki w trójkącie, więc muszą się one przecinać w wierzchołkach. W wyniku przecięcia powstaje na sferze 8 trójkątów sferycznych.

A, B, C -kąty przy odpowiednich wierzchołkach

a, b, c – boki (łuki wyrażone w mierze swoich kątów środkowych) na przeciwko odpowiednich wierzchołków

Suma miar kątów trójkąta sferycznego jest większa od 180 stopni. Wiedział już o tym Menelaos z Aleksandrii (I wiek n.e) - grecki matematyk i astronom. Nadwyżkę sumy miar trójkąta sferycznego nazywa się defektem sferycznym. Dla danej sfery jest on tym większy, im większe jest pole trójkąta sferycznego. Suma kątów trójkąta sferycznego jest mniejsza od 180 stopni.

źródło: apollo.astro.amu.edu.pl

na podstawie: wikipedia.org, "MATeMAtyka" podręcznik dla szkół ponadgimnazjalnych; zakres podstawowy; wydawnictwo Nowa Era

niedziela, 17 maja 2015

Viete

Francois Viete urodził się w 1540 roku w Fontenay-le-Comte we Francji. Po ukończeniu prawa początkowo pracował jako adwokat. Po rozpoczęciu rządów Henryka IV został w 1589 roku radcą Parlamentu w Tours, a później pierwszym radcą królewskim.

Viete zajmował się trygonometrią i algebrą. Wprawdzie do jego czasów w dziedzinie algebry nastąpił już pewien rozwój symboliki i rozwiązywania równań trzeciego i drugiego stopnia poprzez pierwiastkowanie, lecz dopiero on swoimi pracami dał podstawy ogólnej nauce o równaniach algebraicznych.

źródło: www-history.mcs.st-and.ac.uk

Jako pierwszy wprowadził literowe oznaczenia nie tylko dla wielkości niewiadomych, ale i dla wielkości współczynników. W ten sposób dzięki niemu otworzyła się możliwość wyrażania własności równań i ich pierwiastków ogólnymi wzorami. Viete podał ogólne metody rozwiązywania równań drugiego, trzeciego i czwartego stopnia, ujednolicając tym samym metody podane wcześniej oraz wprowadził wzory na sumę i iloczyn pierwiastków równania kwadratowego. Viete był również twórcą zasady dwoistości.

Wszystkie swoje osiągnięcia matematyk zawarł w napisanej w 1591r. pracy "Isagoge in artem analiticam". Drugie jego dzieło jest podstawą geometrii analitycznej. Viete wydawał na swój koszt wiele prac świadczących o jego wielostronnych zainteresowaniach i rozsyłał je do uczelni. Prace te jednak pisane były skomplikowanym językiem i nie rozpowszechniały się w szybkim stopniu. W przeszło czterdzieści lat po śmierci Francois Viete'a dzieła jego zostały wydane pod wspólnym tytułem "Opera Mathematica".

na podstawie: urbanim.republika.pl

środa, 6 maja 2015

Matematyka w sztuce

źródło: butterfield-reignbeau.blogspot.com

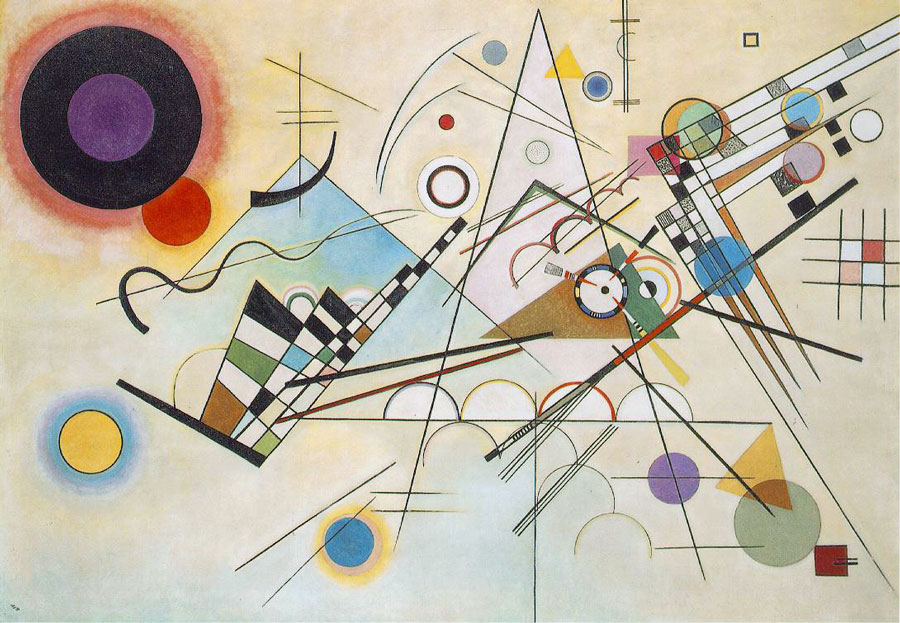
Wassily Kandinsky "Kompozycja VII"

Wassily Kandinsky był pierwszym malarzem tworzącym czysto abstrakcyjne obrazy. Jego prace to przykład zastosowania w sztuce figur geometrycznych.

źródło: pinterest.com

źródło: tate.org.uk

Barbara Hepworth "Orpheus"

Prace tej brytyjskiej rzeźbiarki inspirowane były modelami matematycznymi.

żródło: gazetka_matematyczna.republika.pl

Oto przykład zastosowania motywu wstęgi Möbiusa: szklana rzeźba tak właśnie zatytułowana.

Fraktale

Fraktale to struktury mające w każdej skali podobny, powtarzający się wzór.
Charakteryzuje je samopodobieństwo, co oznacza, że każdy fragment struktury przypomina całość. Wzory fraktalne bywają bardzo urodziwe, ukazują piękno przypadkowych kompozycji, często zachowując jednocześnie symetrię.

źródło: technoblog.computerworld.pl

źródło: tapety.joe.pl

Przykłady fraktali odnajdujemy także w przyrodzie. Mogą nimi być: układ chmur huraganowych, układ gwiazd w galaktyce, układ ziaren w słoneczniku, owoc ananasa, płatki śniegu, drzewo, liść paproci, kryształki lodu, spiralne muszle, szyszki.

Kirigami

Kirigami to odmiana origami, w której wolno twórcy robić małe cięcia w papierze (z jap. kiru – uciąć, kami – papier). W origami tradycyjnym nacięcia nie są używane (uważa się, że techniki składania papieru są wystarczająco rozwinięte, by cięcia nie były potrzebne).

Przykładowe prace:

źródło: pinterest.com

źródło: instructables.com

na podstawie: szkolazklasa2012.ceo.nq.pl/doc/6874/Matematyka_w_architekturze.pptx ; wikipedia.org

poniedziałek, 4 maja 2015

Matematyka w przyrodzie

Liczydło górskie

Ta piękna roślina z grupy konwaliowych nosi swoją matematyczną nazwę nie bez powodu. Jej owoce zdają się przypominać ułożone w rzędach dziesiętnych koraliki szkolnego liczydła. Jest unikatowa w skali Europy, rośnie jednak m.in. na Dolnym Śląsku. Podlega ścisłej ochronie. Kwitnie na przełomie maja i czerwca, a pełnię swojej krasy osiąga w okresie owocowania pod koniec lata.

źródło: pracownia.org.pl

Pięciokąty foremne w... ogrodzie

W pięciokątach foremnych (wypukłym i wklęsłym zwanym pentagramem) kryje się coś szczególnego. Występuje w nich "złota proporcja", to jest taki podział odcinka na dwie części, w którym stosunek całego odcinka do większej części podziału równy jest stosunkowi większej części do mniejszej. Złoty podział występuje powszechnie w przyrodzie, a zwłaszcza tam, gdzie występują foremne pięciokąty.

kwiat bodziszka Endressa

źródło: allegro.pl

Symetria w świecie motyli

W świecie przyrody ożywionej symetria nie jest przypadkiem. Niekiedy po prostu pomaga żyć. Jednym uchem nie można by tak precyzyjnie zlokalizować źródła dźwięku, a jednym okiem - tak dokładnie oszacować odległości. Szczególną uwagę warto zwrócić na motyle. Są to stworzenia, które ideę symetrii realizują w sposób doskonały.

źródło: cenebit.pl

Wyjątkowy świat muszli

Jedną z bardziej interesujących realizacji matematycznych idei w przyrodzie są muszle, które wytwarzają niektóre gatunki mięczaków.Od milionów lat pojawia się na nich wciąż ten sam charakterystyczny rysunek spirali równokątnej. Zastanawiające jest, jakie własności magicznej krzywej sprawiły, że właśnie ten kształt upodobała sobie natura?

na podstawie: szkolazklasa2012.ceo.nq.pl/doc/6874/Matematyka_w_architekturze.pptx

Matematyka w architekturze

Partenon

Świątynia Ateny na Akropolu w Atenach, zbudowana w latach 448-432 p.n.e. Fronton świątyni mieścił się w prostokącie, w którym stosunek boków wyrażał się liczbą złotą.

źródło: wikipedia.org

Krzywa wieża w Pizie

walec

Krzywa Wieża w Pizie, jedna z najbardziej znanych budowli świata, odwiedzana rocznie przez ok. 10 milionów turystów, symbol miasta Pizy. W istocie jest dzwonnicą (kampanilą) katedralną i należy do kompleksu zabudowań w stylu romańskim na Campo dei Miràcoli.

źródło: wikipedia.org

Piramidy w Gizie

ostrosłupy

Piramidy w Gizie to kolejny przykład zastosowania złotego podziału. Jeżeli weźmiemy przekrój Wielkiej Piramidy, to otrzymamy trójkąt prostokątny, nazywany Trójkątem Egipskim. Stosunek przeciwprostokątnej (wysokości ściany bocznej) do podstawy (połowa wymiaru podstawy) wynosi 1,61804 i różni się od złotej liczby tylko o jeden na piątym miejscu po przecinku.

źródło: tajemnicepiramid.w.interia.pl

Zamek w Bytowie

stożek

Zamek w Bytowie – gotycki zamek krzyżacki, następnie książąt pomorskich z XIV-XV wieku. W 1390 roku Krzyżacy zaczęli budować w Bytowie murowany zamek na wzniesieniu w południowo-wschodniej części miasta. Właściwe prace budowlane przeprowadzono jednak w latach 1398-1406 pod kierunkiem Mikołaja Fellensteina. Zamek wzniesiono na planie prostokąta o wymiarach 49x70 m. z kamieni eratycznych i cegły. W narożach powstały 3 okrągłe i jedna kwadratowa wieża.

źródło: osrodek.ibwpan.gda.pl

Matrimandir

kula

Matrimandir (Sanskryt Świątyni Matki) jest indyjskim gmachem o duchowym znaczeniu dla praktyki Integral jogi. Położony jest w centrum Auroville, stworzony z inicjatywy Matek w Sri Aurobindo Ashram. Gmach nazywany jest duszą miasta. Leży w dużej, otwartej przestrzeni określanej nazwą Peace. Matrimandir nie należy do żadnej konkretnej religii lub sekty.